Go big.Int add one performance curiosity

Trying to solve a coding exercise I noticed that doing z.Add(z, one) is kind of slow so I implemented my own increment method :)

Practicing Go by solving the CodeWars exercise “Fabergé Easter Eggs crush test”, I was able to find a simple, and slow solution, by performing many many additions. This simple solution was enough to meet the test requirements but something bugged me from my CPU profilings, z.Add(z, one) was taking cumulative more than one second. In comparison, adding two big numbers was taking cumulative more than five seconds.

For context, the results can have more than 3000 digits so a library which supports those kind of numbers is required. Go standard library provides “math/big” which is an arbitrary-precision arithmetic package and thus it’s the default one and the one I could use in the exercise.

Investigation

In Go investing these kind of issues is easy as doing go test . -cpuprofile=cpu.prof and visualize it with go tool pprof -http :8080 cpu.prof. Which leads us to this:

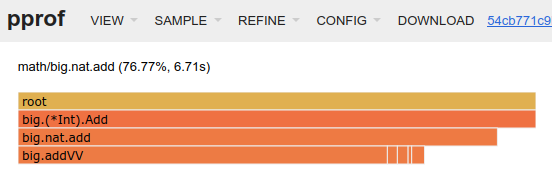
Easy to assume the interesting part is at “nat” an internal type of the “math/big” package. Let’s check the big.nat.add() method:

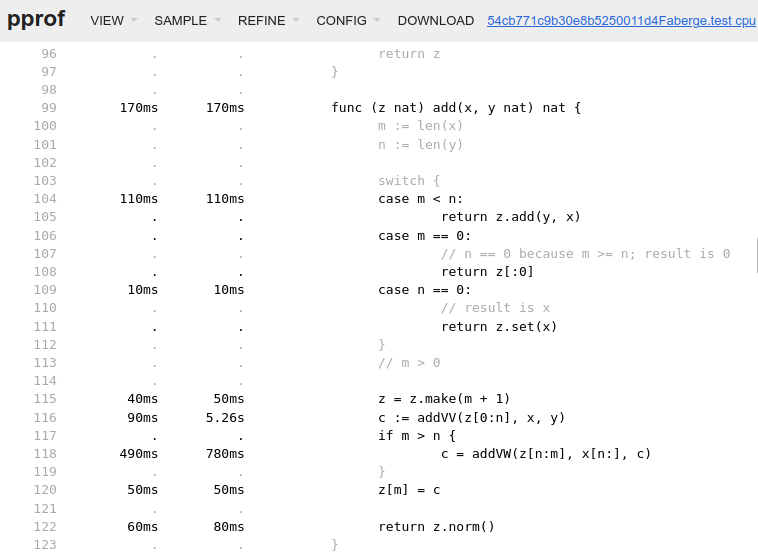
go math.big.nat Copyright 2009 The Go Authors. Check source and license link

Trying to reach conclusions from these metrics is a bit complicated since these metrics show the expected slow adding of two big numbers and also the “unexpected” slow performance of adding one to a big number. Still some ideas can be taken:

• The cumulative time taken on the line c = addVW(z[n:m], x[n:], c) is oddly close to the one second taken by adding one value.
• The switch logic guarantees that the bigger number is always x when actually performing the addition. This means that z.Add(z, one) has the closely the same performance of z.Add(one, z).
• The adding of numbers of different lengths is performed on two steps with addVV() and addVW().
• The bigger the different of lengths between x and y the more “calculations” can be expected from addvw().

Hypothesis 01, a lengthier big.Int

If it is possible to define a big.Int with value 1 but a bigger length that would probably improve performance. Preferably having the same length has “x”, the bigger/lengthier summand, the addition could be performed in one go.

“x”,“y” are big.nat’s which are slices of Word’s so maybe I could create a big.Int with value one but having the bigger slice. This slice would have superfluous zeros to maintain the same value. Checking the big.Int public methods the following method seemed promising.

Still, further checking the called method nat.norm() method this hypothesis gets destroyed.

The resulting slice is cut to remove all superfluous zeros. Checking the nat type description it’s clear that is supposed to always happen.

Hypothesis 02, avoid big.Int.Add()

It seems that big.Int.Add() is following the overall architecture of big.Int and big.nat, supporting adding number of different sizes/lengths and expanding/contracting the results’ slices to remove superfluous zeros so the remaining option seems to be to just avoid using it.

Given that there’s a big.Int.SetBits() and big.Int.Bits() there’s probably a way to implement my own addition/increment. Furthermore, given how Go slices are implemented big.Int.Bits() is probably enough. Read here for more details about this.

Soooo uint(big.NewInt(2).Bits()[0]) == uint(big.NewInt(1).Bits()[0])+1 actually works :)

Solution and benchmark

My increment/add one hack implementation:

The performance graph, same tests, after the hack replaced z.Add(z, one):

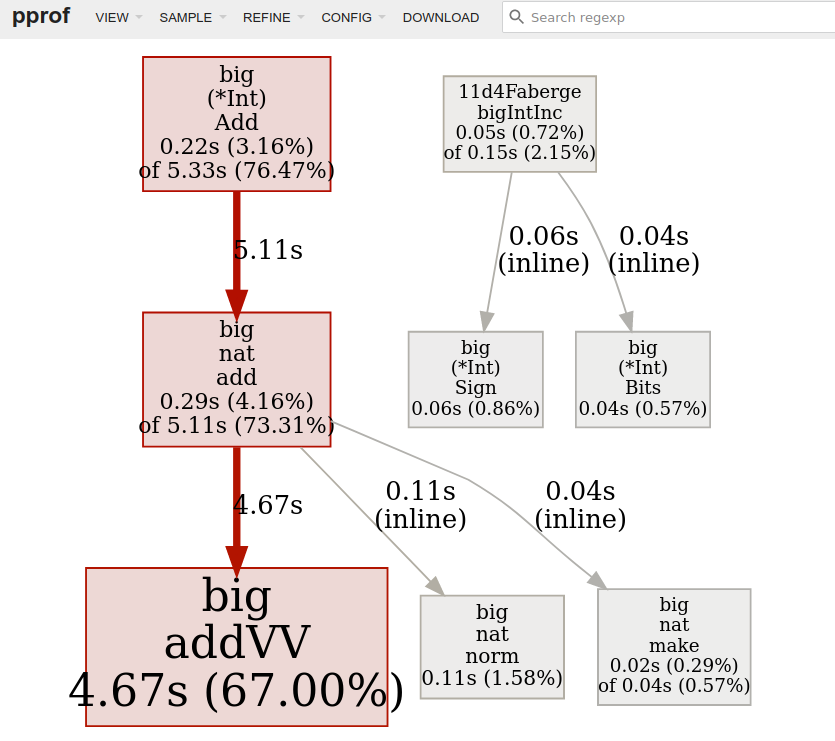
big.Int.Add() was taking 6.71 seconds to now taking 5.11 seconds :)

Notes:

• Overall almost 1.5 seconds was saved from using the bigIntInc().
• The bigIntInc() fallback to call z.Add(z, one) is almost never taken.
• The addVW() method disappeared from the metrics since now only similar lengths numbers are being added.

Extra benchmarks

Since Go has a builtin benchmark tool I decided to try to benchmark this hack. Later I also found about github.com/consensys/gnark-crypto/field which is similar to math/big but optimized for speed so I also benchmarked against it.

user@host$ go test . -run=nothing -bench=. -benchtime=5s
goos: linux
goarch: amd64
pkg: example.com/biigist
cpu: Intel(R) Core(TM) i5-4590T CPU @ 2.00GHz
BenchmarkBigIntInc/512bits_NewInt-4             94064070                57.74 ns/op
BenchmarkBigIntInc/512bits_NewInt_Add-4         64224325                92.77 ns/op
BenchmarkBigIntInc/512bits_NewInt_Inc-4         66054766                92.00 ns/op
BenchmarkBigIntInc/513bits_BIAdd-4              246136504               24.44 ns/op
BenchmarkBigIntInc/513bits_GFAdd-4              447096817               11.57 ns/op
BenchmarkBigIntInc/513bits_Inc-4                1000000000               3.913 ns/op
BenchmarkBigIntInc/1025bits_BIAdd-4             208855520               29.20 ns/op
BenchmarkBigIntInc/1025bits_GFAdd-4             514192068               11.43 ns/op
BenchmarkBigIntInc/1025bits_Inc-4               1000000000               3.905 ns/op
PASS
ok      example.com/biigist     57.451s

Explanation of the results:

• Inc refers to my bigIntInc() method.
• BIAdd refers to big.Int.Add().
• GFAdd refers to gnark-crypto/field Add.
• 512bits_ tests are the worse case for bigIntInc() since the fallback has to be taken. The bench run 512bits_NewInt is to provide the baseline number of creating a new big.Int before each calculation which affects a lot the results.
• 513Bits_ refers to the amount of bits required to represent the base number used in the tests.

You can check the benchmarks at https://github.com/vpereira01/biigist

In conclusion, if you need to increment a big.Int a lot of times for some reason implement a hack :)